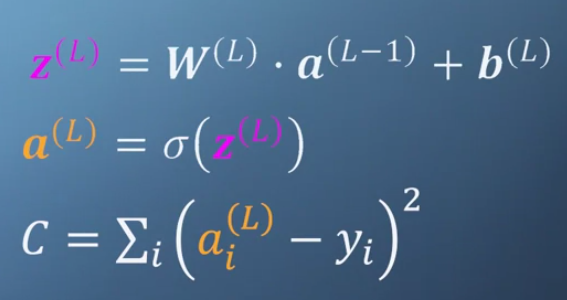240628 Multivariate derivative chain rule with vector or matrix, in Machine Learning

阅前提醒：
本文可能使用了大量比较随便的英文表达；
本文的数学名词、公式可能不严谨；
总之意思传达到就行。

While doing the lab Backpropogation from week 3 of Math for ML course, some questions poped up in my mind.

Some background

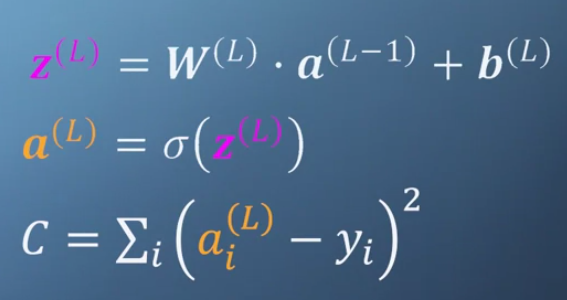
$\boldsymbol{a}^{(L)}$ is the values of the nodes at layer L. $\boldsymbol{a}^{(L)} = [a_0^{(L)}, a_1^{(L)}, \dots, a_{m-1}^{(L)}]$, where m is the number of nodes at layer L.

$z^{(L)}$ is the values before passing to activation function, just a trick to make the derivation of the activation function easier.

$\boldsymbol{W}^{(L)}$ is the weight from layer L-1 to layer L, and $\boldsymbol{b}^{(L)}$ is the bias from layer L-1 to Layer 1.

$\sigma$ is some activation function.

$C$ is the cost function, $y_i$ is the truth value in the dataset for training the network, corresponding to a input $a_i^{(0)}$

What we want to do is to find good $\boldsymbol{W}^{(L)}$ and $\boldsymbol{b}^{(L)}$ that minimize the cost, and for that we need to take partial derivative of $C$ with respect to each W and b.

Questions

In the lab Backpropogation, I doubted a partial derivative formula:

$$\frac{\partial C}{\partial \boldsymbol{W}^{(3)}} = \frac{\partial C}{\partial \boldsymbol{a}^{(3)}} \frac{\partial \boldsymbol{a}^{(3)}}{\partial \boldsymbol{z}^{(3)}} \frac{\partial \boldsymbol{z}^{(3)}}{\partial \boldsymbol{W}^{(3)}}$$

1. Why we can take partial derivative of $C$ with respect to $\boldsymbol{W}$?
2. In the cost function, it sums the squre of $a_i^{(L)} - y_i$, why in the derivative formula it becomes the partial derivative of $C$ with respect to $\boldsymbol{a}$, and how?

Analysis

In the previous lectures, I’ve learned about chain rule for multivariate derivative with function being like this form:

$$f(\boldsymbol{x}(t)), \boldsymbol{x} = [x_1(t), x_2(t), ... x_n(t)]$$

$f$ is a function of $x_1(t), x_2(t), ... x_n(t)$, and each elements of $\boldsymbol{x}$ is a function of $t$, and in the end, $f$ can be a function of $t$. Thus, we can try to find derivative of $f$ with respect to $t$, by using multivariate chain rule:

Equation 1

$$\frac{df}{dt} = \frac{\partial f}{\partial \boldsymbol{x}} \frac{d\boldsymbol{x}}{dt}$$

Equation 2

$$\frac{df}{dt} = \frac{\partial f}{\partial x_1} \frac{dx_1}{dt} + \frac{\partial f}{\partial x_2} \frac{dx_2}{dt} + \dots + \frac{\partial f}{\partial x_n} \frac{dx_n}{dt}$$

The $\frac{\partial f}{\partial \boldsymbol{x}}$ and $\frac{d\boldsymbol{x}}{dt}$ in Equation 1 are vectors, and $\frac{df}{dt}$ is the dot product of these two vectors. The result of dot product just equals to the sum Equation 2. Therefore, we can use the simple form Equation 1.

The independent variable $t$ is a single variable. However, what would the formula be if $t$ is also a pack of variables? e.g.:

$$\boldsymbol{t} = [t_1, t_2]$$

To make it easier for understanding, we can use an example, say $\boldsymbol{x} = [x_1, x_2]$, and $\boldsymbol{t} = [t_1, t_2]$,
$f$ is a function of $\boldsymbol{x}$, $f(\boldsymbol{x})$, (or explicitly $f(x_1, x_2)$, and each element in $\boldsymbol{x}$ is a function of $\boldsymbol{t}$:

$$x = [x_1(\boldsymbol{t}), x_2(\boldsymbol{t})]$$

or explicitly

$$x = [x_1(t_1, t_2), x_2(t_1, t_2)]$$

So, $f$ can be a function of $t_1$ and $t_2$. Now, if we want to find derivative of $f$ with respect to $\boldsymbol{t}$, we have to do partial defferentiation on $t_1$ and $t_2$ respectively:

$$\frac{\partial f}{\partial t_1} = \frac{\partial f}{\partial x_1}\frac{\partial x_1}{\partial t_1} + \frac{\partial f}{\partial x_2}\frac{\partial x_2}{\partial t_1}$$

It can be written as dot product of vector

$$\frac{\partial f}{\partial \boldsymbol{x}} = [\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}]$$

and vector

$$\frac{\partial \boldsymbol{x}}{\partial t_1} = [\frac{\partial x_1}{\partial t_1}, \frac{\partial x_2}{\partial t_1}]$$

Thus,

$$\frac{\partial f}{\partial t_1} = \frac{\partial f}{\partial \boldsymbol{x}}\frac{\partial \boldsymbol{x}}{\partial t_1}$$

And similarly for $t_2$

$$\frac{\partial f}{\partial t_2} = \frac{\partial f}{\partial \boldsymbol{x}}\frac{\partial \boldsymbol{x}}{\partial t_2}$$

Until here, we can roughly answer a part of the question 1:

$C$ is a function of $\boldsymbol{a}^{(L)}$, and $\boldsymbol{a}^{(L)}$ is a function of $\boldsymbol{W}^{(L)}$ and $\boldsymbol{b}^{(L)}$. Therefore, $C$ can also be a function of $\boldsymbol{W}^{(L)}$ and $\boldsymbol{b}^{(L)}$.

Just like above example($f$, $t_1$, and $t_2$), we can take partial derivative of $C$ with respective $\boldsymbol{W}^{(L)}$ and $\boldsymbol{b}^{(L)}$.

However, there is new question:

$\boldsymbol{W}^{(L)}$ is a matrix, how do we take derivative with respect to a matrix?

Key point: derivative with respect to each element in matrix/vector

My idea is that, this is just a simpler form for writing. We can’t take derivative with respect to a matrix or vector, but we actually do that on each element in the matrix or vector.

For the above example $f$, $t_1$, and $t_2$, we can also put $\frac{\partial f}{\partial t_1}$ and $\frac{\partial f}{\partial t_2}$ together in a vector, and write:

$$\frac{\partial f}{\partial \boldsymbol{t}} = [\frac{\partial f}{\partial t_1}, \frac{\partial f}{\partial t_2}]$$

Answer to the question

$C$ is a function of $\boldsymbol{a}^{(L)} = [a_0^{(L)}, a_1^{(L)}, \dots, a_{m-1}^{(L)}]$.

Each $a_i^{(L)}$ is a function of $\boldsymbol{w}_i^{(L)} = [w_{i,0}^{(L)}, w_{i,1}^{(L)}, \dots, w_{i,n-1}^{(L)}]$ and $b_i^{(L)}$. n is the number of nodes in the layer L-1.

We, in fact, are not taking derivative of $C$ with respect to the matrix $\boldsymbol{W}^{(L)}$, but to each variable $w_{i,j}^{(L)}$, while in the end, writing the result as simpler form $\frac{\partial C}{\partial \boldsymbol{W}^{(L)}}$.

Same for $\frac{\partial C}{\partial \boldsymbol{a}^{(L)}}$, we need to take derivative of $C$ with respect to each variable $a_i^{(L)}$, and in the end write as a simpler form.

So let’s start by doing derivative of $z_i^{(L)}$ with respect to $\boldsymbol{w}_i^{(L)}$.

Expan the formula $z_i^{(L)} = \boldsymbol{w}_i^{(L)} \cdot \boldsymbol{a}^{(L-1)} + b_i^{(L)}$:

$$z_i^{(L)} = [w_{i,0}^{(L)}, w_{i,1}^{(L)}, \dots, w_{i,n-1}^{(L)}] \cdot [a_0^{(L-1)}, a_1^{(L-1)}, \dots, a_{n-1}^{(L-1)}] + b_i^{(L)}$$

We can easily get the result of taking derivative of $z_i$ with respect to $w_{i,j}^{(L)}$, it’s just $a_j^{(L-1)}$. But let’s keep these derivative symbols (since the result is not important for our topic) and put all the derivatives in a vector:

Equation 3

$$\frac{\partial z_i^{(L)}}{\partial \boldsymbol{w}_i^{(L)}} = [\frac{\partial z_i^{(L)}}{\partial w_{i, 0}^{(L)}}, \frac{\partial z_i^{(L)}}{\partial w_{i, 1}^{(L)}}, \cdots, \frac{\partial z_i^{(L)}}{\partial w_{i, n-1}^{(L)}}]$$

And then we take derivative of $a_i^{(L)}$ with respect to $z_i^{(L)}$:

$$\frac{\partial a_i^{(L)}}{\partial z_i^{(L)}} = \sigma^{\prime}(z_i^{(L)})$$

Then we do $\frac{\partial C}{\partial a_i^{(L)}}$. Remember that:

$$C = \sum_i (a_i^{(L)} - y_i)^2 = (a_0^{(L)} - y_0)^2 + (a_1^{(L)} - y_1)^2 + \cdots + (a_{m-1}^{(L)} - y_{m-1})^2$$

We only take derivative with respect to $a_i^{(L)}$:

$$\frac{\partial C}{\partial a_i^{(L)}} = 2(a_i^{(L)} - y_i)$$

At last, we can get partial derivative of $C$ respect to each $w_{i,j}^{(L)}$

$$\frac{\partial C}{\partial w_{i,j}^{(L)}} = \frac{\partial C}{\partial a_i^{(L)}}\frac{\partial a_i^{(L)}}{\partial z_i^{(L)}}\frac{\partial z_i^{(L)}}{\partial w_{i,j}^{(L)}}$$

All the derivative term $\frac{\partial C}{\partial a_i^{(L)}}$, $\frac{\partial a_i^{(L)}}{\partial z_i^{(L)}}$, $\frac{\partial z_i^{(L)}}{\partial w_{i,j}^{(L)}}$, are just scalars, so is the result $\frac{\partial C}{\partial w_{i,j}^{(L)}}$.

Now, what if we replace the single variable $w_{i,j}^{(L)}$ with a vector $\boldsymbol{w}_i^{(L)}$?

Then the last term becomes the Equation 3. It is a vector! The first and second term doesn’t change, because we still take derivative with respect to $a_i^{(L)}$ and $z_i^{(L)}$.

So what happens to $\frac{\partial C}{\partial w_{i,j}^{(L)}}$? It also turns to a vector!

$$\frac{\partial C}{\partial \boldsymbol{w}_i^{(L)}} = [ \frac{\partial C}{\partial w_{i,0}^{(L)}}, \frac{\partial C}{\partial w_{i,1}^{(L)}}, \cdots, \frac{\partial C}{\partial w_{i, n-1}^{(L)}} ]$$

What is $\boldsymbol{w}_i^{(L)}$? It is the ith row of the matrix $\boldsymbol{W}^{(L)}$. If we then do similar things to each row of $\boldsymbol{W}^{(L)}$, and stack them together, we get a new matrix, that is $\frac{\partial C}{\partial \boldsymbol{W}^{(L)}}$!

$$\frac{\partial C}{\partial \boldsymbol{W}^{(L)}} = \begin{bmatrix} \frac{\partial C}{\partial \boldsymbol{w}_0^{(L)}} \\ \frac{\partial C}{\partial \boldsymbol{w}_1^{(L)}} \\ \vdots \\ \frac{\partial C}{\partial \boldsymbol{w}_{m-1}^{(L)}} \end{bmatrix}$$

Take away

When there is vector or matrix in a derivative formula, we are taking derivative with respect to each element in matrix or vector.